VERIFICA MOTORE

PREMESSA

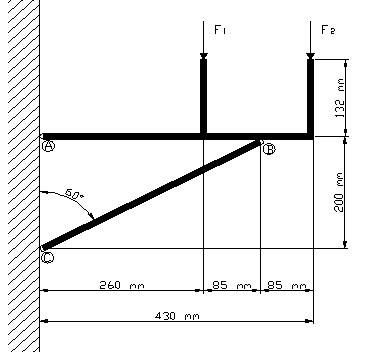
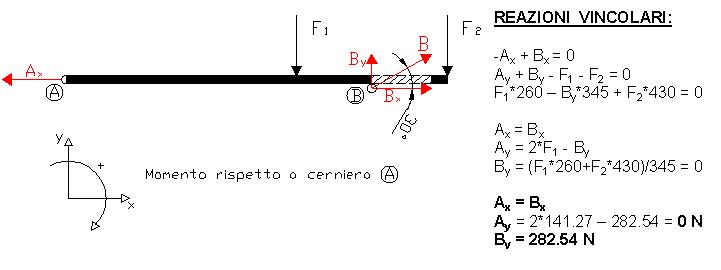
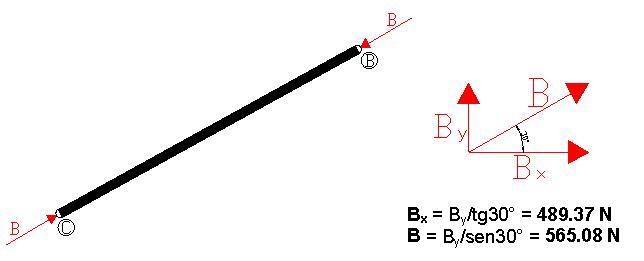
In questa prova si va a verificare che la struttura che sorregge il motore riesca a resistere a determinate sollecitazioni ed a determinati carichi.
Tenendo presente che il suddetto motore poggia su quattro travi verticali ad L che, a loro volta, vengono sorrette da una mensola formata anch'essa da travi a L; tenendo conto che il peso del motore viene scaricato equamente nella struttura portante, la forza che solleciterà ognuna delle quattro travi verticali sarà un quarto del peso dell'intero motore.
La verifica è stata fatta tenendo conto che il peso del motore è sottoposto ad accelerazioni durante le fasi di decollo ed atterraggio; è per questo motivo che lo si è moltiplicato per il coefficiente di contingenza n1.

DATI

MATERIALE:
AW 6061T4
E = 70000 N/mm2
sr = 235 N/mm2
ss = 140 N/mm2
n = coefficiente di sicurezza = 3
n1 = coefficiente di contingenza = 2
CARICHI:
m = massa totale motore
mtot = msecco + melica + mscarichi = 28.8 kg
Ftot = peso totale motore
Ftot = mtot*g = 28.8*9.81 = 282.53 N

FORZE

Schema

La figura rappresenta la struttura portante del castello motore, questa la si può ancora semplificare. Di seguito è rappresentata la struttura ulteriormente semplificata:

Schema semplificato

F1 = F2 = (Ftot/4)*n = (Ftot/4)*2 = Ftot/2 = 282.53/2 = 141.27 N

REAZIONI VINCOLARI

Reazioni vincolari

Come è noto dai calcoli, le due forze (F1 ed F2) sono equilibrate dalla componente verticale della forza B; conoscendo questa componente, è possibile trovare il valore della forza B e della sua componente orizzontale Bx.
Si osservi lo schema delle forze seguente:

Puntone

SOLLECITAZIONI AMMISSIBILI

samm = ss/n = 140/3 = 46.7 N/mm2
tamm = samm/(3)1/3 = 27 N/mm2

BARICENTRO E MOMENTO D'INERZIA

Sono stati adottati come travi, dei profilati ad "L" del tipo 30X30X4. Tale tipologia di profilato ha le seguenti caratteristiche geometriche (in realtà presenta raggi di piega e di raccordo, ma non ne si tiene conto perché hanno una scarsa rilevanza nel calcolo dei valori statici).
n
Xi
Yi
Ai
AiXi
AiYi
1
15
2
120
1800
240
2
2
17
104
208
1768
SOMMA
  
224
2008
2008

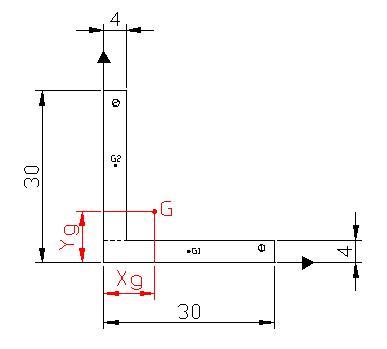
Baricentro

CALCOLO DEL BARICENTRO
Le coordinate del baricentro dell'intero profilato ad L sono:
Xg = 2008/224 = 8.96 mm
Yg = 2008/224 = 8.96 mm
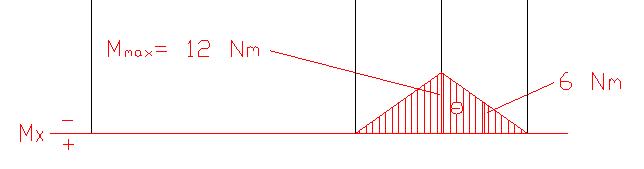
Ne consegue che Ymax per calcolo della resistenza al momento flettente sarà
Ymax = L – Yg = 30 – 8.96 = 21.04 mm

CALCOLO DEL MOMENTO D'INERZIA MINIMO
Il calcolo è stato eseguito per un unico profilato a L.
Imin= [1/12 × (30×43 + 4×263 )] + 30×4× (8.96-2)2 + 26×4× (17-8.96)2 = 18554 mm4

VERIFICA A TAGLIO

TAGLIO MASSIMO
Tmax= F1 = F2 = ± 141.27 N
DIAGRAMMA SFORZO DI TAGLIO

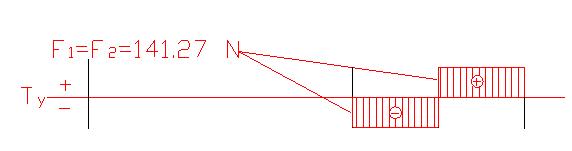
Diagramma Taglio

SOLLECITAZIONE UNITARIA
Si considera solo la sezione verticale in quanto si presume che essa assorba la maggior parte degli sforzi di taglio; quindi non viene applicata la formula: tmax = Tmax*Wx / (I*b)
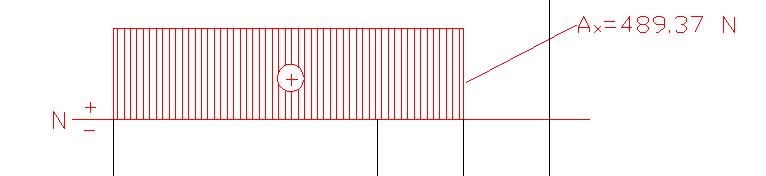
A = area resistente
A = 30 × 4 = 120 mm2
tmax = (3 × T)/(2×A) = (3 × 141.27)/(2×120)= 1.8 N/mm2
MARGINE DI SICUREZZA
Ms = tamm/ttmax -1 > 0
Ms= 27/1.8 - 1 = 14

VERIFICA A SFORZO NORMALE

DIAGRAMMA SFORZO NORMALE

Diagramma sforzo normale

smax = N/Ai = 489.37/((30*4)+(26*4)) = 489.37/484 = 1 N/mm2
MARGINE DI SICUREZZA
Ms = samm/smax -1 > 0
Ms= 46.7/1 - 1 = 45.7

VERIFICA A MOMENTO FLETTENTE

MOMENTO MASSIMO
Mmax = -141.27 * 85 = - 11895 Nmm = 12 Nm
M = momento flettente

Diagramma Momento Flettente

SOLLECITAZIONE UNITARIA
smax = Mmax/Wx = (Mmax × Ymax)/Imin
smax = (11895 × 21.04)/18554 = 13.5 N/mm2
MARGINE DI SICUREZZA
Ms = samm/smax -1 > 0
Ms= 46.7/13.5 - 1 = 2.5

VERIFICA A sid

s IDEALE
sid = (s2 + 3*t2)1/2=13.9 N
MARGINE DI SICUREZZA
Ms = samm/sid -1 > 0
Ms= 46.7/13.9 - 1 = 1.4

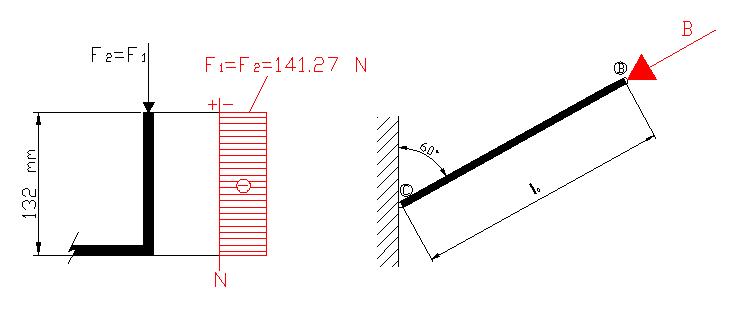
VERIFICA A CARICO DI PUNTA

VERIFICA A CARICO DI PUNTA

Carico di punta

lo = (3452 + 2002)1/2 = 398.78
Fcr = (p2 × E × Imin)/lo2 = (p2 × 70000 ×18554)/398.782 = 80606.23 N
B < Fcr
565.08 < 61776.2
Indaur