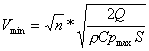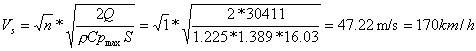Diagramma di manovra

        I carichi agenti su di un velivolo sono molto vari, in quanto dipendono  dal tipo di velivolo, dalle condizioni di volo e dalla volontà del pilota, nonché, dalla necessità (si pensi, ad esempio, ad una manovra di disimpegno durante un combattimento). Una volta in volo questi carichi devono essere sopportati dalle strutture resistenti del velivolo, le quali sono state progettate appositamente per questo scopo. Le dimensioni di queste strutture, rivestono un elemento fondamentale nella progettazione del velivolo: una struttura molto resistente implica l’impiego di una grande quantità di materiale, di spazio e, soprattutto, di peso. Nel campo aeronautico, il peso di un velivolo è un fattore chiave, in quanto questo condiziona in maniera determinante  le prestazioni e la tipologia costruttiva dello stesso.

Facendo un paragone con un’autovettura, è semplice comprendere come  più questo mezzo è grande e pesante, più potente deve essere il propulsore che lo spinge, e più grande è il propulsore e più aumenta il peso. Si instaura così un circolo, dal quale è possibile uscire solo attuando una politica di compromesso.

Per ottimizzare al meglio i pesi e le potenze da impiegare, ogni aereo viene progettato per ricoprire un determinato ruolo, per il quale vengono previste tutte le possibili condizioni operative. Il costruttore, quindi, imposta valori come la velocità massima, il tipo di profilo da utilizzare, il tipo di armamento o di bagaglio da dover trasportare… Sulla base delle specifiche impartite, si passa alla determinazione di quelle che possono essere le sollecitazioni massime che la struttura si troverà a dover subire, ed in base a queste al dimensionamento della struttura stessa.

Il valore massimo delle sollecitazioni ammissibili, è fortemente influenzato dalla natura dell’uomo: sottoposto a determinate manovre, il corpo del pilota deve resistere ad elevate accelerazioni, le quali, a seconda che spingano il sangue dalla testa verso i piedi o viceversa vengono dette positive o negative. Queste accelerazioni vengono normalmente indicate in base ad un rapporto tra l’accelerazione stessa e quella gravitazionale, ottenendo così un numero che viene chiamato “numero di g”.

Da diversi studi eseguiti sulla natura umana, è stato ricavato che, un uomo, in condizioni normali, cioè sprovvisto degli attuali giubbotti anti g, può sopportare un numero massimo di g pari a 7.

Per fornire un esempio pratico, se un pilota del peso di 700N si trovasse a dover sopportare 7 g, il suo corpo peserebbe 4900N. Questo aumento di peso apparente comporta problemi alla circolazione  sanguigna con una conseguente possibile perdita di conoscenza.

            Con l’introduzione delle tute anti g, i piloti possono  sopportare un numero massimo di g pari ad 11, ma negli anni ’30, cioè nel periodo in cui è stato progettato il Bf. 109, questi sistemi di protezione non esistevano. Per questo motivo tutta la struttura di questo aereo è stata progettata per sopportare accelerazioni positive massime di 7g e negative di 3.5g, cioè per i massimi valori sopportabili dall’organismo umano.

Come già anticipato, la portanza può non essere orientata nella stessa direzione del peso in tutte le manovre, ma comunque ne contrasta una componente rilevante. Come per il corpo umano, anche il peso apparente dell’aeromobile aumenta sensibilmente durante manovre ad alto numero di g, e questo costringe i piloti ad aumentare la portanza, in modo da compensare l’aumento di peso. Il massimo valore della portanza ammissibile si avrà, quindi, nelle condizioni in cui questa è orientata nella stessa direzione del peso durante una manovra al massimo numero di g consentito. Se il pilota, in queste condizioni, tentasse di aumentare la portanza (magari per uscire da una discesa molto ripida o per stringere il più possibile una virata) la struttura sarebbe chiamata a sopportare uno stress superiore a quello per cui è stata progettata, e questo potrebbe portare al cedimento della  stessa o ad una sua deformazione permanente. In entrambi i casi, comunque, l’integrità del velivolo verrebbe gravemente compromessa.

Tutte le parti strutturali del velivolo vengono quindi progettate tenendo conto di un  fattore di sicurezza “k” per il quale viene moltiplicato il numero massimo di g ammissibili (in questo caso 7) ottenendo il numero di g per il quale la struttura verrà progettata.

            Per i principi relativi alle condizioni di volo a regime, ad un aumento di peso apparente deve corrispondere un aumento di portanza, in modo da riportare la situazione nelle condizioni di equilibrio. L’aumento di portanza può essere ottenuto dal pilota agendo su due fattori: il Cp e la V. In particolare, un aumento del coefficiente di portanza potrebbe essere ottenuto incrementando l’incidenza dell’ala, e quindi del profilo che la costituisce. Aumentare l’incidenza significherebbe porre l’aereo in un assetto più cabrato, variando così l’angolo formato tra la corda del profilo e la direzione del vento relativo. Il pilota, però, non può permettersi di modificare l’incidenza a piacimento, in quanto ogni profilo possiede un Cp massimo, oltre al quale avviene lo stallo, condizione nella quale si ha la perdita, più o meno repentina, delle  caratteristiche aerodinamiche del profilo e, quindi, interrompendo tutti quei fenomeni che originano la portanza.

D’altro canto, ottenere un decisivo aumento di velocità in maniera abbastanza repentina è quasi impossibile a causa delle caratteristiche costruttive del motore, il quale, oltre ad un limite relativo al numero di giri massimo, deve far fronte anche ad un limite della potenza disponibile. Si noti, inoltre, che un aumento di incidenza, oltre che aumentare il Cp, farebbe aumentare anche il Cr, incrementando così, anche la potenza necessaria al volo. Comunque, anche se non venissero considerate le limitazioni derivate dal motore, un eccessivo aumento della velocità potrebbe portare alla formazione di una portanza superiore a quella consentita, facendo collassare la struttura resistente del velivolo (nella fattispecie quella delle ali).

               Queste considerazioni assumono una notevole importanza soprattutto nella prima parte del volo (cioè nelle condizioni di decollo e di salita, dove le basse velocità e le alte incidenze  costringono i piloti a compiere manovre relativamente “tranquille”, in modo da non aumentare troppo il peso apparente), e nelle condizioni di volo veloce, dove la velocità è così alta che un aumento troppo elevato del coefficiente di portanza potrebbe portare al collasso della struttura. A questo proposito, è stato creato un particolare diagramma, chiamato diagramma di manovra, nel quale  viene tracciato l’inviluppo di volo di un determinato velivolo.

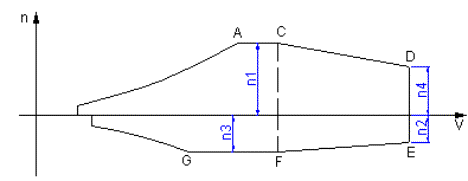
Le norme che regolano le condizioni di sicurezza per il volo sono abbastanza recenti, e comunque posteriori alla seconda Guerra Mondiale, cioè al periodo in cui è “nato” il 109, ma i primi grafici di manovra erano già presenti anche in quegli anni, e le norme che li regolavano sono simili a quelle utilizzate tutt’oggi. Con una certa approssimazione, sarà possibile ricostruire il diagramma di manovra del 109, utilizzando le attuali norme.

Creazione del diagramma di manovra

            Il diagramma di manovra non è altro che una rappresentazione su piano cartesiano delle condizioni ammissibili per il volo in sicurezza: sulle ascisse vengono indicate le velocità di volo, mentre sulle ordinate sono riportati i valori dei fattori di carico.

Con il temine “fattore di carico” viene indicata un’entità di cui si è già parlato in precedenza, e cioè il numero di g. Infatti, il fattore di carico, generalmente indicato con “n”, è dato dal rapporto tra la portanza sviluppata in un determinato momento ed il peso effettivo del velivolo. È facile intuire che, se l’aereo sviluppa una portanza  pari a  sette volte il suo peso, per essere in equilibrio il velivolo dovrebbe aumentare di sette volte il suo peso, e questo aumento può essere dato solo dall’azione delle accelerazioni agenti sul velivolo stesso, le quali incrementano il peso effettivo con il peso apparente. Quindi, il valore risultante dal rapporto prima citato è proprio quello dell’accelerazione a cui il velivolo è sottoposto. Per questo motivo, è lecito scrivere   

  [f.04]

Il valore massimo ammissibile del fattore di carico viene detto fattore di contingenza, e per questo aereo è pari a 7 per accelerazioni positive e 3.5 per accelerazioni negative. Il valore del  limite massimo della velocità di un aeromobile viene invece indicato con la sigla  Vne[1], mentre quello minimo, cioè la velocità di stallo, con la sigla Vs.

            Il grafico di manovra può essere diviso in due parti principali: una prima parte, nella quale le basse velocità non permettono al velivolo di affrontare manovre con un elevato fattore di carico, ed una seconda parte, dove, fino al limite massimo della velocità di crociera Vc, è possibile affrontare qualsiasi manovra fino ad n = 7, ed oltrepassato questo limite le velocità sono così elevate che si è costretti a limitare i valori del fattore di carico massimo ammissibile per non compromettere l’integrità strutturale

            Per la costruzione della prima parte del grafico si procede nel seguente modo: ricordando che, per le condizioni di equilibrio, la portanza deve essere uguale al peso, ponendo a sistema la [f.01] e la [f.04] si otterrà che  

[f.05]  

Esplicitando da questa formula la velocità di volo V si otterrà:

[f.06]

Considerando che in condizioni di decollo Q, S, r e Cp assumono valori constanti (trascurando il consumo di carburante e ponendo il valore di Cp uguale a quello massimo possibile per il profilo utilizzato, che per il velivolo Bf. 109, risulta essere  pari a 1.389), si avrà che la velocità minima di sostentamento dipenderà esclusivamente dal valore di n secondo la formula 

 [f.07]

Ricordando la [f.04], risulta che il valore normale di n è 1, in quanto in queste condizioni la portanza dovrà essere uguale al peso; per questo motivo nella determinazione della velocità minima di sostentamento  il valore di n che dovrà essere inserito nella [f.07] sarà 1.

Sostituendo  ad n valori che vanno da 1 a 7, si determineranno le velocità minime da assumere per ogni manovra ad un determinano fattore di carico. Riportando questi punti sul di un piano cartesiano, ed unendoli con una curva, si traccerà la prima parte del diagramma relativo alle accelerazioni positive.

Per fare un esempio, definito il peso del velivolo Q pari a 30411N e la superficie alare S = 16.03 m², la velocità di stallo, cioè quella calcolata con n = 1, sarà:

Valori minimi delle velocità di manovra al variare di n per accelerazioni positive

Con lo stesso procedimento si potrà determinare la curva delle velocità minime relative alle accelerazioni negative, ricordando che il Cp negativo massimo è pari a 1.055 e che il fattore di contingenza per queste accelerazioni risulta 3.5.

Valori minimi della velocità di manovra al variare di n per accelerazioni negative

Si potrà quindi calcolare la velocità di crociera “Vc” del velivolo: data la Vne, cioè la velocità massima consentita, ottenuta in una picchiata con un angolo di discesa pari a 30°, è possibile calcolare la velocità massima su di una traiettoria orizzontale “V_maxVOR”, la quale è pari alla Vne divisa per 1.3[2]:

Dalla V_maxVOR è possibile ricavare la velocità di crociera, in quanto questa è pari ai nove decimi della velocità massima orizzontale. Per determinare la Vc, quindi, basterà moltiplicare la V_maxVOR per 0.9, ottenendo

Questa velocità assume un’importanza notevole ai fini del volo, in quanto è la velocità  che un aereo assume per percorrere la massima distanza possibile.

            Ricapitolando, i punti fondamentali per il diagramma di manovra determinati sino a questo momento sono sei: il punto “S”, individuato dalle coordinate (Vs; n = 1); il punto “A”, le cui coordinate sono costituite dal valore del fattore di contingenza positivo e dalla velocità minima relativa a questa sollecitazione (Va; n₁); il punto “C”, rappresentato da (Vc; n₁); in punto “H”, con velocità Vsr[3] e massimo fattore di carico negativo n₃[4] (Vsr; n₃); il punto “G”, corrispondente alla minima velocità con cui può essere affrontata una manovra con il massimo fattore di carico negativo Vg[5] ed il massimo fattore di carico negativo (Vg; n₃) ed il punto “F”, con coordinate (Vc; n₃). Resta quindi da tracciare solo la parte finale del grafico di manovra, cioè quella relativa alle alte velocità.

            Anche se il Bf. 109 è stato progettato per resistere ad una manovra eseguita alla massima velocità ed al massimo fattore di carico ammissibile, i costruttori tendono a sconsigliarne l’esecuzione, in quanto, una qualsiasi turbolenza incontrata in queste condizioni porterebbe la struttura a sopportare sollecitazioni che superano quelle massime ammissibili, portando al collasso della struttura. Per questo motivo alle alte velocità, si consiglia di non oltrepassare mai un fattore di carico massimo indicato con n₄ per le accelerazioni positive ed n₂ per quelle negative.

In genere, n₄ ed n₂ vengono considerati pari al 75% dei rispettivi n₁ ed n₃, quindi, eseguendo un rapido calcolo, si determina che

A questo punto sono disponibili quindi anche le ultime due coordinate mancanti del diagramma di manovra, le quali vanno ad individuare il punto “D” (Vne; n₄) ed il punto “E” (Vne; n₂). Unendo ora con segmenti rettilinei i punti A, C, D, E, F e G la costruzione del diagramma di manovra sarà terminata.

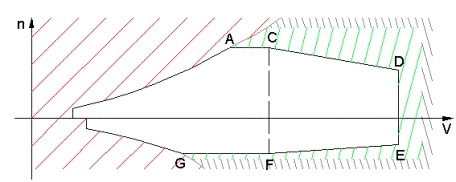
Le curve costruite secondo le modalità esposte rappresentano il perimetro del diagramma di manovra: l’area interna ed esso costituisce l’insieme di tutti i possibili assetti con i quali l’aeromobile è in grado di volare senza sottoporre la struttura resistente ad eccessive sollecitazioni.

Significato del diagramma di manovra

L’area esterna a questo diagramma rappresenta l’insieme di tutti quegli assetti di volo dannosi o proibiti per il velivolo. In particolare, prolungando le curve SA ed HG, lo spazio esterno al diagramma verrà diviso in due parti: la prima parte, compresa tra l’asse delle ordinate e le due curve appena citate rappresenta la zona di stallo; la seconda parte, compresa tra le due curve ed un’ipotetica linea verticale passante per un punto con velocità superiore alla Vne, rappresenta l’insieme degli assetti pericolosi per la struttura.

 Nella prima parte, quella dello stallo, il velivolo, date le sue condizioni di bassa velocità ed alte incidenze, non è in grado di sviluppare una portanza pari al proprio peso, o, comunque, se tentasse di incrementare ancora la portanza aumentando l’incidenza, ricadrebbe nello stallo, perdendo completamente la portanza agente sulle sue ali a causa del distacco della vena fluida. Il volo in condizioni di equilibrio in questa zona è quindi impossibile.

Nella seconda parte, invece, le sollecitazioni che la struttura sarebbe richiamata a sopportare andrebbero oltre al limite massimo imposto dal costruttore. Quest’aerea di grafico, comunque, è sostanzialmente divisa in due parti: una prima parte, consistente in una fascia posta a contatto con il perimetro del diagramma di manovra e dotata di una determinata ampiezza, ed una seconda parte, che si estende esternamente alla prima. Nella fascia attigua al diagramma di manovra, lo stress a cui è sottoposta la struttura non è così elevato da creare danni, in quanto, come detto in precedenza, la struttura stessa viene sovradimensionata per motivi di sicurezza con l’ausilio di appositi coefficienti “k”. Gli assetti compresi in questa fascia, quindi, non sono molto dannosi per la struttura, anche se esulano dal diagramma di manovra. La tensione limite di snervamento funge da confine a questa fascia di relativa sicurezza, costituendo il confine invalicabile delle deformazioni elastiche. Una volta che i carichi agenti sul velivolo hanno superato questo valore, le deformazioni della struttura diventano permanenti: questo sta a significare che la struttura del velivolo è irrimediabilmente compromessa, ed un aumento delle sollecitazioni potrebbe portare al suo collasso.

            Alla base del diagramma di manovra, e quindi, di tutte le considerazioni fatte fino a questo momento, sta l’ipotesi che il velivolo stia manovrando in aria calma, e cioè in assenza di turbolenza.

Come è logico pensare, le condizioni di volo in aria agitata sono contraddistinte da un aumento dei parametri di sicurezza, con una conseguente diminuzione dei valori massimi ammissibili riguardanti velocità di volo e fattore di carico.

Per il volo in queste condizioni è stato studiato un apposito diagramma, chiamato diagramma di raffica, alla base del quale sta il diagramma di manovra.

Il Diagramma di raffica

            Il diagramma di raffica, come il diagramma di manovra, restituisce visivamente, per mezzo di un grafico, l’insieme di tutte le condizioni di volo per le quali la resistenza della struttura del velivolo non viene messa a repentaglio, garantendo un certo margine di sicurezza.

Questo diagramma, comunque, offre solo una soluzione parziale al problema costituito dalle improvvise turbolenze che possono essere incontrate, infatti, prevede che il pilota, attraverso l’aiuto di bollettini meteo o, comunque, di stazioni a terra, eviti le zone di maggiore turbolenza. 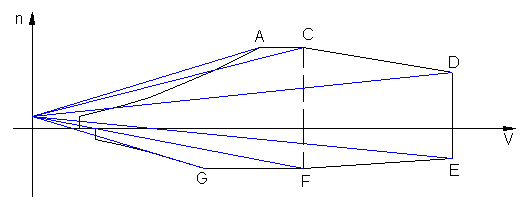Oltre a questo fattore, resta da dire che il valore massimo delle raffiche considerate è il risultato di una media di valori registrati, e che, quindi, non rappresenta in assoluto il massimo di un’ipotetica ma alquanto improbabile turbolenza.

Detto ciò, è possibile passare alla realizzazione di questo diagramma: dalle norme ICAO, cioè le norme che stabiliscono le minime condizioni di volo ammissibili per gli aerei civili, si ricava che, facendo riferimento al diagramma di manovra precedentemente realizzato, i punti A e G rappresentano gli assetti ai quali un aeromobile può sopportare la massima raffica, la quale, sempre secondo queste norme, sarebbe caratterizzata da una velocità ascendente o discendente di circa 20 m/sec. I punti C ed F, invece, rappresentano gli assetti limite per una raffica di 15.25 m/sec, ed i punti D ed E quelli per una raffica di 7.60 m/sec.

Conducendo dei segmenti rettilinei dal punto di coordinate (V = 0; n = 1) ai sei punti considerati si otterrà il diagramma di raffica. Questi segmenti rappresentano il valore massimo di raffica, e l’area del diagramma di manovra compresa tra due segmenti aventi lo stesso valore di raffica rappresenta l’insieme degli assetti “sicuri” per il volo in aria turbolenta con un valore delle velocità delle correnti ascendenti o discendenti minore di quello del segmento considerato.

Come per il diagramma di manovra, volare con assetti posti al di fuori dell’area di sicurezza del diagramma di raffica può portare al collasso della struttura, cosa che, considerando gli effetti di correnti ascensionali o discensionali molto violente, potrebbe avvenire in modo molto più rapido ed imprevedibile rispetto al volo in aria calma.